Краткий теоретический материал по 2-3 деревьям

См. оригинал здесь.

Определение

• Пустое дерево и дерево с одной вершиной являются 2-3 деревьями.
• Каждая внутренняя вершина (не корень) имеет два или три сына.
• Листья содержат ключи и связанную с ними информацию.
• Все листья упорядочены слева направо в отношении строгого порядка (<). Ключ любого листа меньше его правого брата, и больше его левого. # В каждом внутреннем узле есть три ссылки на его сыновей (возможно nil). А также ключ наименьшего элемента, являющегося потомком его второго сына, и ключ наименьшего элемента, являющегося потомком его третьего сына.
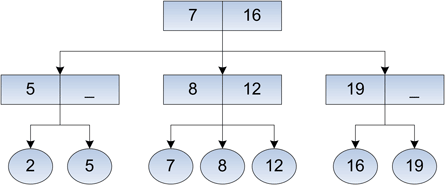
  Рис. 1. Пример 2-3 дерева. Таким образом, 2-3 дерево с _k_ уровнями имеет от _2^{k + 1}_ до _3^{k - 1}_ листьев. Или 2-3 дерево с _n_ вершинами имеет не менее _1 + log₃n_ уровней и не более _1 + log₂n_ уровней. Таким образом, длина любого пути от корня до листа имеет порядок _O(log₂n)_.

Поиск

Пусть имеем ключ _x_, найдем связанную с ним информацию (она находится вместе с ключом в некотором листе). Начиная с корня, входим во внутреннюю вершину с ключами _y_, _z_ (возможно nil, если сыновей нет). Если _x < y_, необходимо перейти к первому сыну вершины. А если _y <= x < z_, то перейти ко второму. И наконец, если _x <= z_, то перейти к третьему, и так до листа. !!!Вставка элемента!!! Пусть нам необходимо поместить новый элемент с ключом _x_. Мы двигаемся как и при поиске до внутренней вершины, предшествующей листьям. Если эта вершина имеет 2 сыновей, (то нам повезло) добавляем третий лист с соответствующей коррекцией вершин. Заметим, однако, что эта коррекция охватывает только вершины от листа до корня (в худшем случае). Пусть мы заносим ключ 18 в дерево на рис. 1. Имеем: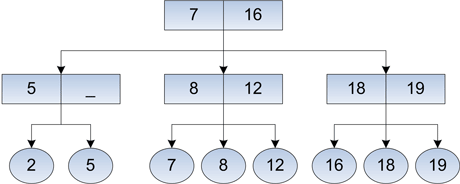
Рис. 2. После добавления ключа 18. Хуже, однако, когда пытаемся занести во внутреннюю вершину уже имеющую трех сыновей (листьев). Итак, элемент _x_ — четвертый. Добавим его к этой вершине node. Получим четыре листа. Теперь расщепим вершину node на две: _node_ и _node\'_. Два наименьших ключа войдут в _node_, два других — в _node\'_. Далее процесс продолжается к родителю _node_ — _p_. Если _p_ имела два сына, то в _node\'_ будет третьим с коррекцией ключей в вершинах. Если же _p_ имела трех сыновей, то расщепляем _p_ на _p_ и _p\'_ и т.д. до корня. Корень — особый случай. В этом случае корень р расщепляем на _p_ и _p\'_ и создаем новый корень с двумя сыновьями _p_ и _p\'_. Количество уровней в последнем случае увеличится на 1. Например: добавление ключа 10 к 2-3 дереву на рис. 2.
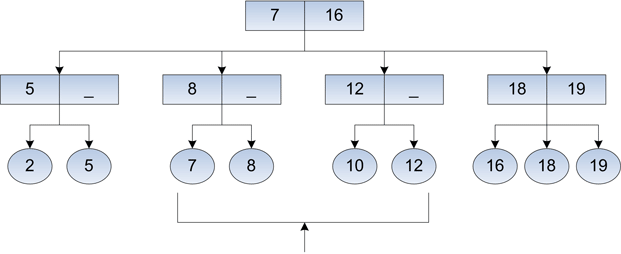
Рис. 3. Добавление ключа 10. Мы расщепили эту пару. Однако нужно расщепить и родителя этой пары (рис. 4). Родитель — корень.
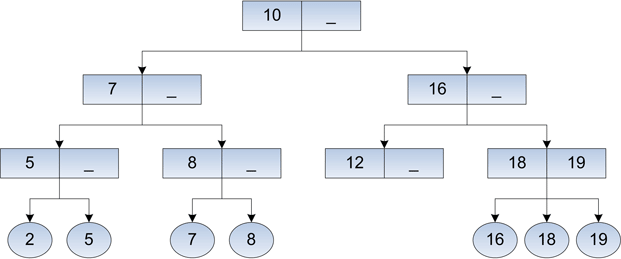
Рис. 4. Расщепление при добавлении ключа 10. Итак, при занесении нового ключа может возникнуть расщепление вершин, если у родителя появилось 4 вершины (серия рисунков 2, 3, 4). Однако, посмотрим на рис. 2 при добавлении ключа 10. В вершине четыре листа, но его левый брат имеет два сына. Тогда можно отдать ему наименьший ключ. Аналогично с правым братом. Это — переливание из одной вершины в другую. Тогда при добавлении к дереву рис. 2 ключа 10 мы получим следующее дерево (рис. 5):
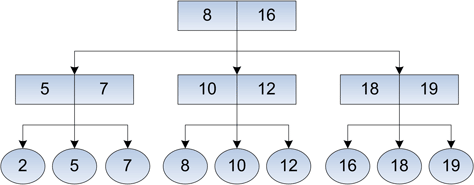
Рис. 5. Финальный вид дерева после добавления ключа 10.

Удаление

При удалении листа его родитель _node_ может остаться с одним сыном. Если вершина _node_ — корень, то он остается с единственным сыном. Если же _node_ — не корень, то пусть его родитель _р_. Если родитель имеет другого сына, расположенного слева или справа от _node_, и этот сын имеет трех сыновей — то переливание, эта вершина с тремя сыновьями отдает одного своему брату _node_, и обе они теперь будут иметь двух сыновей. Если же брат _node_ имеет двух сыновей, то сын _node_ становится сыном брата _node_. Брат _node_ теперь будет иметь трех сыновей (слияние), а вершина _node_ освобождается. Например, удаление ключа 10 из дерева на рис. 4. За счет слияния получим (рис. 6.):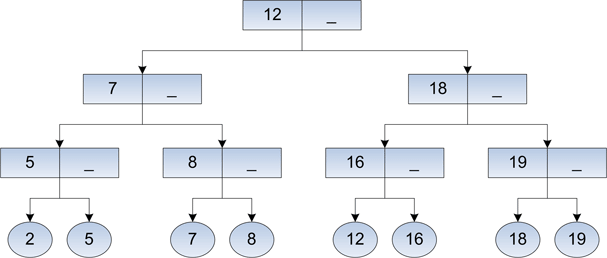
Рис. 6. Слияние вершин при удалении ключа 10. Пусть теперь из дерева на рис. 6 удалим ключ 7 (рис. 7).
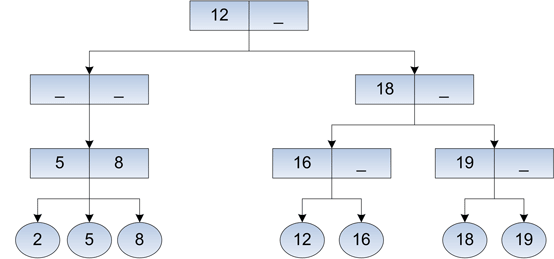
Рис. 7 (a). Удаление ключа 7.


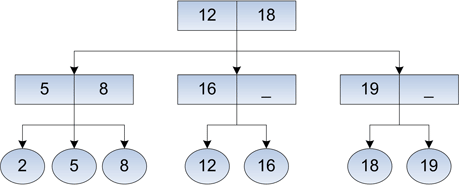
Рис. 7 (б). Удаление ключа 7.